今回は令和3年(2021年)法規の問13を解いていきます。
負荷率・需要率・不等率の問題ですね
苦手意識がすっごいある、覚えにくいし。。。
本番でも(b)間違えてたし。。。
ではやっていきましょう

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋
問題

解法
(a)
まずは負荷率・需要率・不等率の整理ですね
下記のような関係になります。
法規の問題だとよく出ると思います。
今回みたいに何個かを組み合わせて解いていく問題は
10年に1回くらいでしょうか?
\(\displaystyle 負荷率=\frac{平均需要電力}{最大需要電力}\)
\(\displaystyle 需要率=\frac{最大需要電力}{負荷設備容量の合計}\)
\(\displaystyle 不等率=\frac{各負荷の最大需要電力の合計}{合成最大需要電力}\)
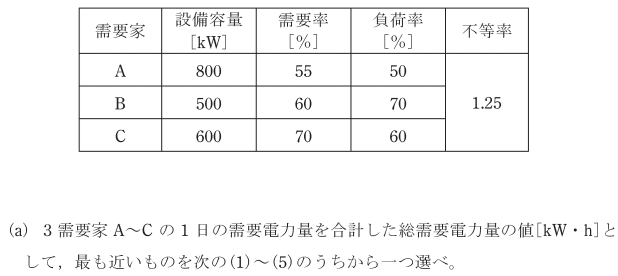
問題はこちら。AからCの1日の総需要電力量の値[kw・h]を求めよ
平均需要電力を出して24hをかければよい
負荷率を使って
\(\displaystyle 負荷率=\frac{平均需要電力}{最大需要電力}\)
\(\displaystyle 平均需要電力=負荷率×最大需要電力\) ①
最大需要電力出して負荷率かければいいね!
最大需要電力がわかりませんね。
需要率を使って
\(\displaystyle 需要率=\frac{最大需要電力}{負荷設備容量の合計}\)
\(\displaystyle 最大需要電力=需要率×負荷設備容量の合計\) ②
左から2つを掛け算すると最大需要電力になりますね!
平均需要電力は ①に②を代入して。。。
\(\displaystyle 平均需要電力=負荷率×需要率×負荷設備容量の合計\)
左から3つを掛け算すると平均電力になりますね!
忘れたときにダメもとでやってみてください
となります。
実際に計算してみると
| 設備容量 kW | 需要率 % | 負荷率 % | 最大需要電力 kW 設備容量×需要率 | 平均需要電力 kW 最大需要電力×負荷率 | |
| A | 800 | 55 | 50 | 800×0.55=440 | 440×0.5=220 |
| B | 500 | 60 | 70 | 500×0.60=300 | 300×0.7=210 |
| C | 600 | 70 | 60 | 600×0.70=420 | 420×0.6=252 |
となりました。
AからCの1日の総需要電力量の値[kw・h]は
各工場の平均需要電力を足して24hをかけると。。。
\(\displaystyle =(220+210+252)kW×24時間=16368kW・h\)
になります。
正解は(2)です
(b)


奥さん。総合負荷率ですってよ!
本番で間違えたのよね
負荷率は
\(\displaystyle 負荷率=\frac{平均需要電力}{最大需要電力}\)
で、、、各工場の総合負荷率だから
\(\displaystyle 負荷率=\frac{各工場の平均需要電力合計}{合成最大需要電力}\)
だな!!
各工場の平均需要電力合計は各工場の平均需要電力は出したから足せばよい
\(\displaystyle =(220+210+252)kW=682kW\)
合成最大需要電力は未知!!
需要率の出番ですね
\(\displaystyle 不等率=\frac{各負荷の最大需要電力の合計}{合成最大需要電力}\)
\(\displaystyle 合成最大需要電力=\frac{各負荷の最大需要電力の合計}{不等率}\)
\(\displaystyle 合成最大需要電力=\frac{440+300+420}{1.23}=943.08kW\)
ってことは、数値を代入して
\(\displaystyle 負荷率=\frac{682kW}{943.08kW}=72.3%\)
正解は(4)ですね
おまけ(b)問題 ながしーのミス
不等率の式がちょっとあいまいになってました。。。悔しい
本来なら下記の式なのですが
\(\displaystyle 不等率=\frac{各負荷の最大需要電力の合計}{合成最大需要電力}\)
\(\displaystyle 不等率=\frac{負荷設備容量の合計}{合成最大需要電力}\)
って間違えてやっちゃってました。
間違えて覚えないように文字を小さくしておきますね
気づいたのは次の日の夕方でしたね。
それまでは何で間違えた理由がわからずにずっともやもやしていました。
基本に立ち返るのは大事ですね!

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋



コメント