今回は令和1年(2019年)理論の問8を解いていきます。
電源が二個あるので重ね合わせの理を用いて求めていきます。
電源一個づつで考えて解いていく手法です。

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋
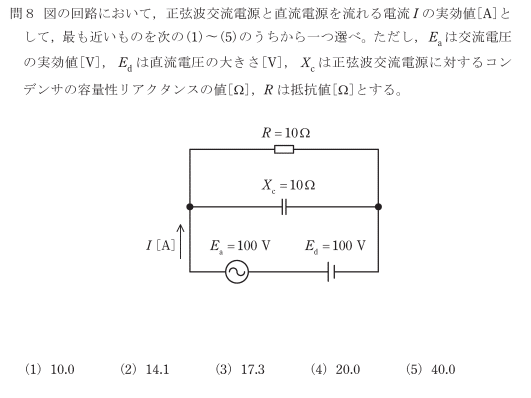
直流電源側だけ抜き出して考える
直流電源だけ抜き出します
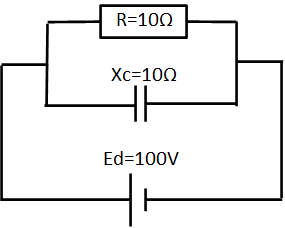
次に直流の定常状態だとコンデンサに電流は
流れないので。。。
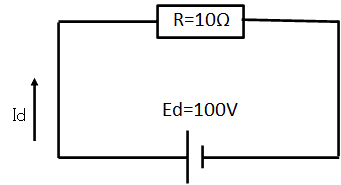
こうなります。
\(\displaystyle E_a=RI_d\)
\(\displaystyle I_d=\frac{E_a}{R}=\frac{100V}{10Ω}=10A\)
交流電源だけ抜き出して考える
交流電源だけ抜き出しました
ん。。。。コンデンサの単位がオームなんだけど。。。。?!?!
\(\displaystyle F(ファラッド)=\frac{s(時間)}{Ω(オーム)}\) でした!
\(\displaystyle Z_c=-\frac{1}{j \omega [1/s] C[s/Ω]}=-\frac{1}{j\omega C}Ω=j10Ω\)
ちゃんとオームになっているのね。。。
周波数ωはすでに10Ωの中に入っていると。。。
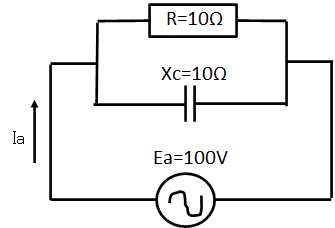
次に合成インピーダンスZを求めていきます
並列なので和分の積で求めます
\(\displaystyle \dot Z=\frac{jRX_c}{R+jX_c}\)
次に\(\dot Z\)の大きさを求めます
\(\displaystyle Z=\frac{RX_c}{\sqrt{R^2+X^2_c}}\)
\(\displaystyle Z=\frac{10\times 10}{\sqrt{{10}^2+{10}^2}}\)
\(\displaystyle ~~=7.071Ω\)
電流の大きさ
\(\displaystyle I_a=\frac{E_d}{Z}=\frac{100}{7.071}=14.14A\)
重ね合わせの理なので 電流を重ねる
〇非正弦波交流の実効値
\(\displaystyle I=\sqrt{I^2_0+I^2_1+I^2_2+・・・+I^2_n+}\)
\(I:非正弦波交流の実効値\)
\(I_0:直流成分の実効値\)
\(I_1:基本派の実効値\)
\(I_k:第k高調波の実効値\)
らしい。よくわからんです
さてさて、この公式を使って電流を求めます
\(\displaystyle I=\sqrt{I^2_d+I^2_a}=\sqrt{10^2+14.14^2}=17.32A\)
正解は3になります。

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋



コメント