今回は令和1年(2019年)理論の問2を解いていきます。
久々にコンデンサの問題を見るとビビりますね。
しっかりと抑えていきましょう。

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋
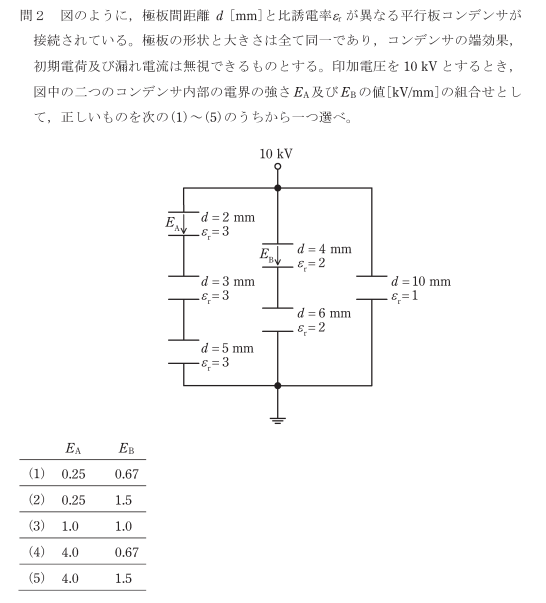
コンデンサの電界を求める問題です。
わかりにくいのでコンデンサに番号を付けました。
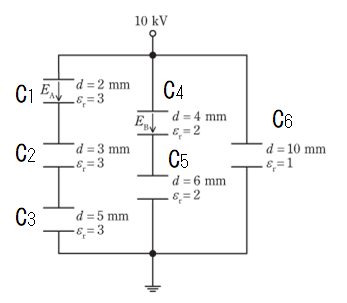
\({E_A}\)解法
まずは\(E_A\)から求めていきます。
コンデンサが直列で\({C_1 C_2 C_3}\)が接続されています。
直列ですので電荷\(Q_1 Q_2 Q_3\)は等しいです。
プラスとマイナスの電荷がお互い1SETになっているので
コンデンサが直列の場合は電荷Qは等しいのです。
\(Q_1=Q_2=Q_3\)
次にわかっている式を立てていき、\(E_A\)を求めていきます
\(V_1+V_2+V_3=10[kV]\)
\(V=Ed\)なので
\(E_Ad_1+E_2d_2+E_3d_3=10[kV]\)
次に\(E_AとE_2 E_3\)の関係を求めます。
結論から言うと、直列に接続したコンデンサの
電荷Q、誘電率ε、面積Sが等しければ電界Eも等しいです
\(E_A=E_2=E_3\)となります。別途下のほうで説明します。
\(E_Ad_1+E_Ad_2+E_Ad_3=10[kV]\)
\(E_A(d_1+d_2+d_3)=10[kV]\)
数値を代入
\(E_A(2mm+3mm+5mm)=E_A(10[mm])=10[kV]\)
\(\displaystyle E_A=\frac{10[kV]}{10[mm]}\)=1[kV/mm]
となります。
\(E_B\)解法
次は\(E_B\)です。解き方は一緒です。
\(V_4+V_5=10[kV]\)
\(V=Ed\)なので
\(E_Bd_4+E_5d_5=10[kV]\)
電荷Q、誘電率ε、面積Sが等しいので
(E_B=E_5)となります。別途下のほうで説明します
\(E_Ad_4+E_Bd_5=10[kV]\)
\(E_A(d_4+d_5)=10[kV]\)
数値を代入
\(E_A(4mm+6mm)=E_A(10mm)=10[kV]\)
\(\displaystyle E_B=\frac{10[kV]}{10[mm]}\)=1[kV/mm]
よって正解は(3)になります。
おまけ(電荷Q、誘電率ε、面積Sが等しければ電界Eも等しい)
なぜ電界が等しいのか。。。?
コンデンサ関係の基本的な式は
\(\displaystyle Q=CV\)——1
\(\displaystyle C=\frac{\epsilon S}{d}\)——-2
1に2を代入
\(\displaystyle Q=\frac{\epsilon S}{d}V\)
→\(\displaystyle V=\frac{dQ}{\epsilon S}\)—3
\(V=Ed\)
→\(\displaystyle E=\frac{V}{d}\)—-4
4に3を代入
\(\displaystyle E=\frac{Q}{\epsilon S}\)
さてEがわかりました。
右辺を見てみると
電界Q 誘電率ε コンデンサの面積Sが残っています。
ですので、コンデンサは電界Q 誘電率ε コンデンサの面積S
が等しければ電界Eも等しくなるのです

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋



コメント