R1(2019年)理論　問16　 第三種電気主任技術者試験（電験三種）丁寧に解いていく（過去問解法）（国家資格）

今回は令和1年（2019年）理論の問16を解いていきます。

対称三相交流の問題です

解き方がわかっちゃえばすごい簡単ですね

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋

問題

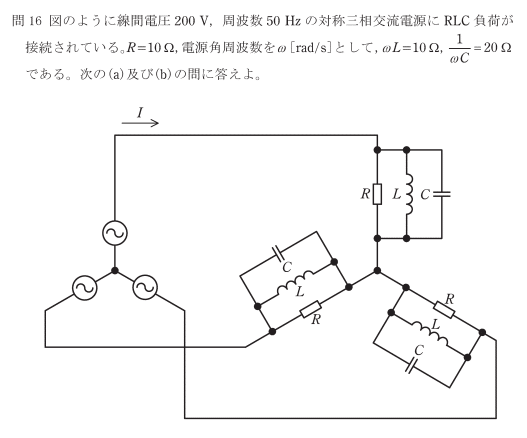
(a)解法

対称三相交流なので中心部分は電位0Vになります

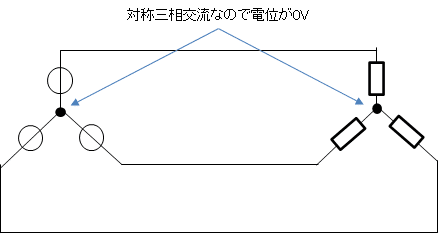
そのため、下記のようなイメージになります線でつなげちゃう

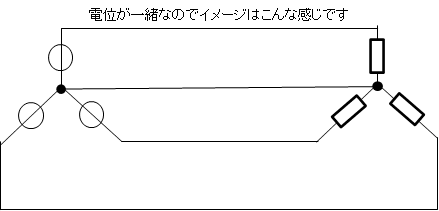
一相分だけ考えれば良いというわけです

今回の問題だとこんな感じです
これなら解けそうですね！

まずは合成インピーダンスを求めます
\(\displaystyle \dot Z=\frac{1}{\frac{1}{R}+\frac{1}{j\omega L}+j\omega C}\)

数字を先に代入します。計算ミスしそうなので。。。
\(\displaystyle \dot Z=\frac{1}{\frac{1}{10}+\frac{1}{j10}+j\frac{1}{20}}\)

\(\displaystyle ~~~~=\frac{1}{\frac{1}{10}+\frac{1}{j10}+j\frac{1}{20}}\)

\(\displaystyle ~~~~=\frac{1}{\frac{1}{10}-\frac{j}{10}+j\frac{1}{20}}\)

\(\displaystyle ~~~~=\frac{1}{\frac{1}{10}-j\frac{1}{20}}\)

\(\displaystyle ~~~~=\frac{1}{0.1-j0.05}\)

次に合成インピーダンスの大きさを求めます
\(\displaystyle Z=\frac{1}{\sqrt{(0.1)^2+(0.05)^2}}\)

\(\displaystyle ~~~~=\frac{1}{0.1118}\)

\(\displaystyle ~~~~=8.9445\)

インピーダンスの大きさがわかったので電流を求めます
今は一相分で考えているので
\(\displaystyle E=\frac{200}{\sqrt{3}}\)です。

\(\displaystyle I=\frac{V}{R}=\frac{\frac{200}{\sqrt{3}}}{8.9445}\)
\(\displaystyle ~~~~=12.9A\)

正解は(3)です

(b)解法

有効電力と書いてあるので、電力消費を考えるのは抵抗RだけでOKです
また、三相分と書いてあるので注意してください

有効電力の式
\(\displaystyle P=3相分\times R{I_R}^2\)

むむ、、、\(I_R\)がわからないので求めます。

\(\displaystyle I_R=\frac{E}{R}\)
なので

\(\displaystyle P=3\times R{(\frac{E}{R}})^2\)

\(\displaystyle ~~~=3\times {\frac{E^2}{R}}\)

\(\displaystyle ~~~=3\times {\frac{{(\frac{200}{\sqrt{3}}})^2}{10}}\)

\(\displaystyle ~~~=4000W=4.0kW\)

正解は(4)です

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋