今回は令和1年(2019年)理論の問12を解いていきます。
またコンデンサの問題ですね
理論らしい問題だと思います。こういう問題、苦手です。

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋
問題
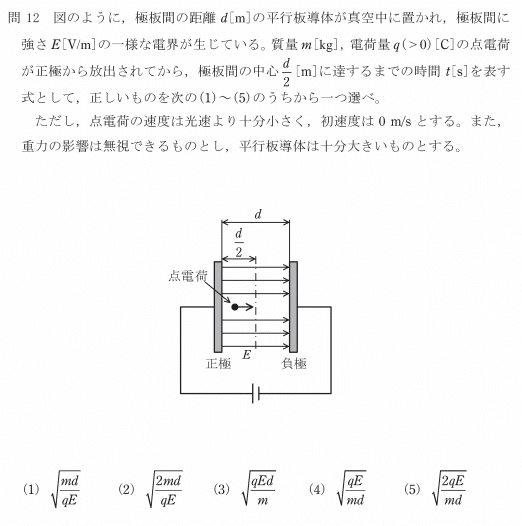
解法
ややこしい問題ですね。
問題を読むのも嫌になる。。。
到達するまでの時間を求めます。
初速度が0m/sなので加速度を求めていきましょう
\(F=ma\)
\(力[N]=質量[kg]×加速度[m/s^2]\)
Fを求める式は、、、
F=qE
\(力[N]=電荷[C]×電界[V/m]\)
\(\displaystyle F=qE=q_1\frac{q_2}{4\pi ε r^2}=\frac{q_1q_2}{4\pi ε r^2}\)
こういうことね!
2つの式を使って求めていきます
\(\displaystyle ma=qE\)
\(\displaystyle a=\frac{qE}{m}\)
加速度がわかったので次は時間を求めていきます。
\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)
\(x:移動距離m、x_0:今いる距離m、V_0:初速度v/s、t:時間s、a:加速度\)
※忘れちゃったら加速度をtで積分していけば導出できます。
\(a=a_0→v=v_0+at→x=x_0+v_0t+\frac{1}{2}at^2\)
\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)
\(\displaystyle x_0=0、v_0=0なので。。\)
\(\displaystyle x=\frac{1}{2}at^2\)
\(\displaystyle t^2=\frac{2mx}{qE}\)
\(\displaystyle t=\sqrt{\frac{2mx}{qE}}\)
数値を代入すると
\(\displaystyle t=\sqrt{\frac{md}{qE}}\)
正解は(1)になります

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋



コメント