今回は令和3年(2021年)法規の問11を解いていきます。
支線にかかる引っ張り荷重の問題ですね
過去問にもよく出ているの解けるようにしておかないとですね。
簡単だし得点源です!!

B問題は得点源 A問題は運ゲー!!

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋
問題
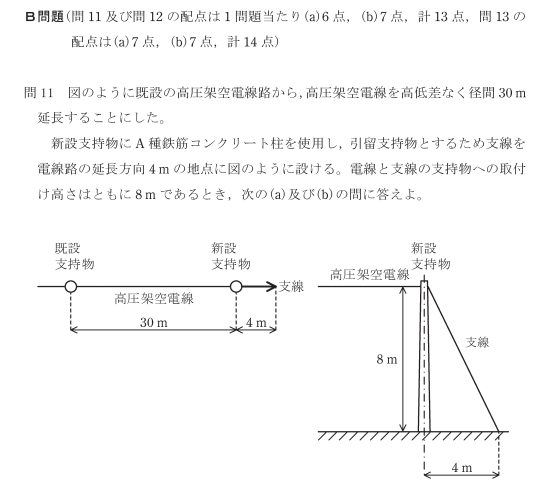

解法
(a)
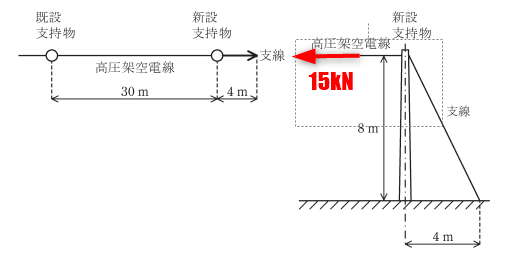

支線側にも水平に15kNがかかって釣り合ってるから。。。
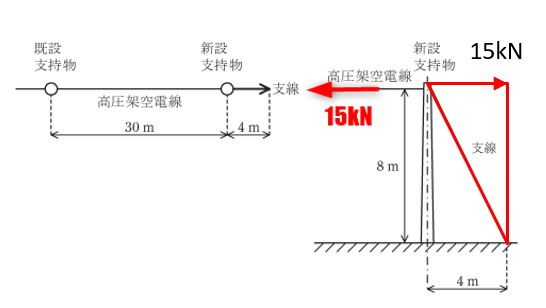
赤線の三角形の斜めのところの長さを計算するよ
\(\displaystyle 斜めの長さ=\sqrt{8^2+4^2}\)
\(\displaystyle =\sqrt{64+16}=8.944\)
三平方の定理(ピタゴラスの定理)直角三角形
\(\displaystyle c^2=a^2+b^2\)
\(\displaystyle c=\sqrt{a^2+b^2}\)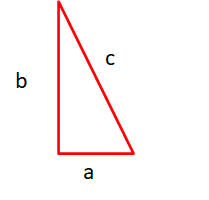
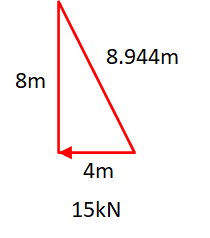
となります。
長さの比と力がかかってる所の比は一緒だから
\(\displaystyle 支線にかかる張力:15kN=8.922m:4m\)
\(\displaystyle 支線にかかる張力=15kN×\frac{8.944}{4}\)=33.54kN\)
比で計算してます
なんで正解は33.54kNなので (4)34kN ですね
(b)

安全率1.5だから 支線は 33.54kNより 1.5倍強い
支線じゃないといけません
\(\displaystyle 33.54kN×1.5=50.31kN\)
次、素線の強度を求めます
\(\displaystyle 素線の強度=\frac{(2.9mm)^2}{2^2}×PI()×1.23kN/mm^2\)=8.12kN
\(\displaystyle 断面積=\frac{直径D^2}{2^2}×PI()\)
半径×半径×πです
1本当たりの素線の強度がわかったので
素線が何本必要か求めます
\(\displaystyle 素線の必要本数=\frac{50.31kN}{8.12kN}=6.19本≒7本以上あればOK\)
ということで正解は(3)7です

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋



コメント