今回は平静22年(2010年)法規の問11を解いていきます。
変流器の構造がわかっていないとわからない問題ですね!
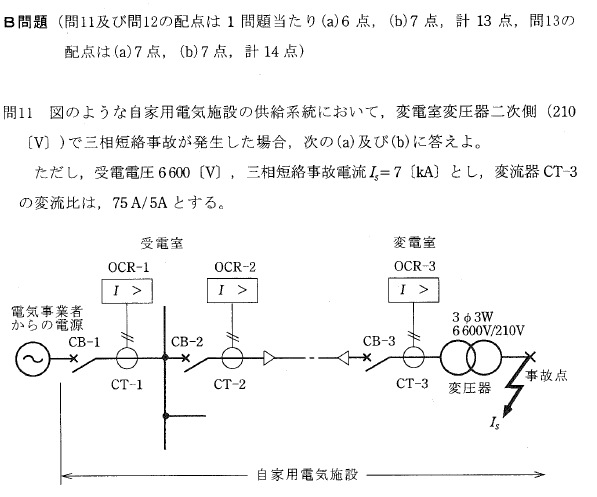

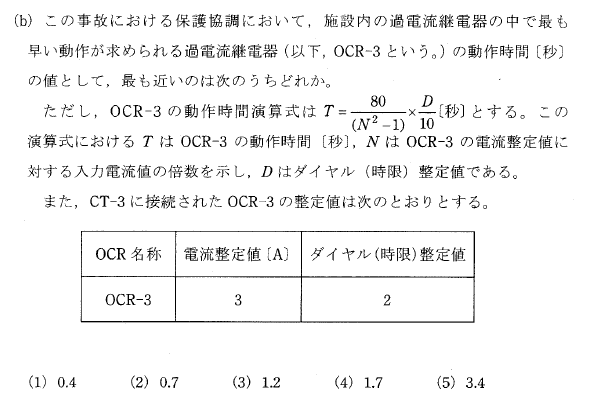

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋
(a)解答

下図だと変流器CTのイメージがわかりにくいので
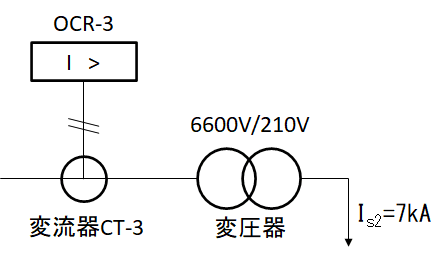
下図に変更します。
初め、意味が分からなかったのですが
CTは計測器小電流を送る装置でした。
\(I_{S1}\)を\(I_{S12}\)という弱い電流に変換してから計測器に送るもの
※変圧器と同じ原理ですね!
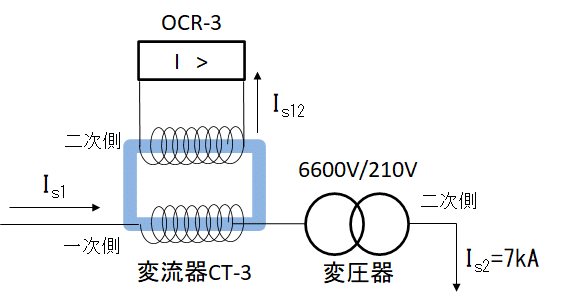
問題は事故時における整流器CT-3の二次電流ですので図で言う
\(I_{s12}\)のことです。
この順番で解いていきます。
①\(I_{s2}\)から\(I_{s1}\)を算出
②\(I_{s1}\)から\(I_{s12}\)を算出
①\(I_{s2}\)から\(I_{s1}\)を算出
三相短絡事故電流\(I_{s2}=7kA\)
変圧器の二次側にあるので一次電流\(I_{s1}\)に換算します。
変圧器の一次側、二次側の電圧電流の関係は
\(\displaystyle \frac{V_2}{V_1}=\frac{I_1}{I_2}\)
\(V\)が大きくなれば\(I\)が小さくなる
\(V\)が小さくなれば\(I\)が大きくなる
または、一次側の電力と二次側の電力は変わらないので
P=\(V_1I_1=V_2I_2\)
と覚えてください
なので
\(\displaystyle \frac{V_2}{V_1}=\frac{I_{s1}}{I_{s2}}\)
\(\displaystyle I_{s1}=\frac{V_{2}}{V_{1}}I_{s2}\)
\(\displaystyle I_{s1}=\frac{210V}{6600V} \times7000A=222.7A\)
と一次電流\(I_{s1}\)が求まりました。
②\(I_{s1}\)から\(I_{s12}\)を算出
CT-3の変流比は 一次側75A/二次側5A です
そのため
\(\displaystyle I_{s12}=\frac{5A}{75A} \times222.7A=14.848A\)
となります
整流器CT-3の二次電流\(I_{s12}\)を求めることができました
正解は(4)14.9になります
(b)解答

\(\displaystyle T=\frac{80}{N^2-1} \times{\frac{D}{10}}秒\)と与えられています
Dはダイヤル(時限)整定数と書いてあるので
D=2
NはOCR-3の電流整定値に対する入力電流値の倍数と書いてあるので
電流整定値:3A
入力電流値:\(I_{s12}=14.848A\)
\(\displaystyle N=\frac{14.848A}{3A}=4.949\)
\(\displaystyle T=\frac{80}{(4.949)^2-1} \times{\frac{2}{10}}=0.681秒\)
正解は(2)0.7 となります。
最後に
記事にすると理解が深まります。
ただし、すごい疲れます 笑

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋



コメント