r3年電力 問2第三種電気主任技術者試験
流体の問題です。
式をよく覚えておけば問題ないかと思います。
試験前に公式を確認しましょう!!
問題
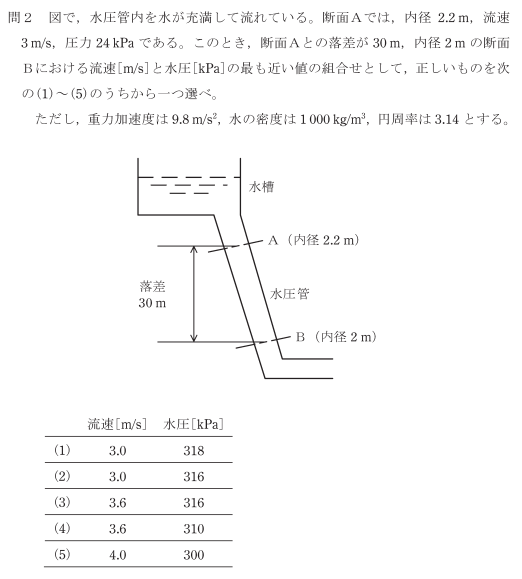
流速を求める
連続の式を使って解いていきます
非圧縮流体の連続の式
\(\rm \displaystyle Sv=const\)
圧縮流体の連続の式
\(\rm \displaystyle ρSv=const\)
const:一定の値を取る
ρ:流体の密度[kg/m3]
S:管の断面積[m/s]
v:流体の速度[m2]
密度が1000kg/ m3 と記載されているので
密度は固定、非圧縮流体ですね!!
非圧縮流体の連続の式を使って流速を求めます
\(\rm \displaystyle Sv=const\)
constなのでA,Bの位置で同じ数値になるので
\(\rm \displaystyle S_Av_A= S_Bv_B\)
\(\rm \displaystyle v_B=\frac{S_Av_A}{S_B}\)
\(\rm \displaystyle =\frac{\frac{{2.2}^2m\times \pi}{4}\times 3m/s }{\frac{{2}^2m\times \pi}{4}}\)
\(\rm \displaystyle =\frac{{2.2}^2m\times 3m/s}{{2}^2m}\)
\(\rm \displaystyle =\frac{{2.2}^2m\times 3m/s}{{2}^2m}\)
=3.63m/s
水圧を求める
次はベルヌーイの式を使用して流速を求めます
ベルヌーイの式
\(\rm\displaystyle P+\frac{1}{2}ρ{v}^2+ρgz=const\)
P:管の圧力[Pa]
ρ:流体の密度[kg/m3]
S:管の断面積[m/s]
v:流体の速度[m2]
g:重力加速度[m/s2]
z:高さ[m]
覚え方
P+運動エネルギー+位置エネルギー=const
でmをρに変える。。。エネルギー保存の法則ですね。
\(\rm\displaystyle P:Pa=J/m^3 単位体積当たりの圧力エネルギー?\)
\(\rm\displaystyle \frac{1}{2}ρ{v}^2:\frac{1}{2}m{v}^2に似ているので運動エネルギー\)
\(\rm\displaystyle ρgz:mghに似ているので位置エネルギー\)
単位はすべてJ/m^3ですので単位体積当たりのエネルギーになっていると思います
A、Bの位置のエネルギーは等しいのでA、Bの位置のエネルギーは等しいので
\(\rm\displaystyle P_A+\frac{1}{2}ρ{v_A}^2+ρgz_A=P_B+\frac{1}{2}{v_B}^2+ρgz_B\)
式を移動して、数値を代入して解いていく
\(\rm\displaystyle P_A+\frac{1}{2}ρ{v_A}^2+ρg(z_A-z_B)=P_B+\frac{1}{2}{v_B}^2\)
\(\rm\displaystyle 24\times10^3+\frac{1}{2} \times 1000\times 3^2+1000\times 9.8\times 30=P_B+\frac{1}{2} \times 1000\times {3.63}^2\)
\(\rm\displaystyle 24000+4500+294000=P_B+6588.45\)
\(\rm\displaystyle P_B=315911Pa=315.9kPa\)
正解は(3)です



コメント