r3年理論 問15第三種電気主任技術者試験
コンデンサの問題です。ながしーは苦手だなぁ
公式などをちゃんと覚えていれば
多分解けると思います。
問題
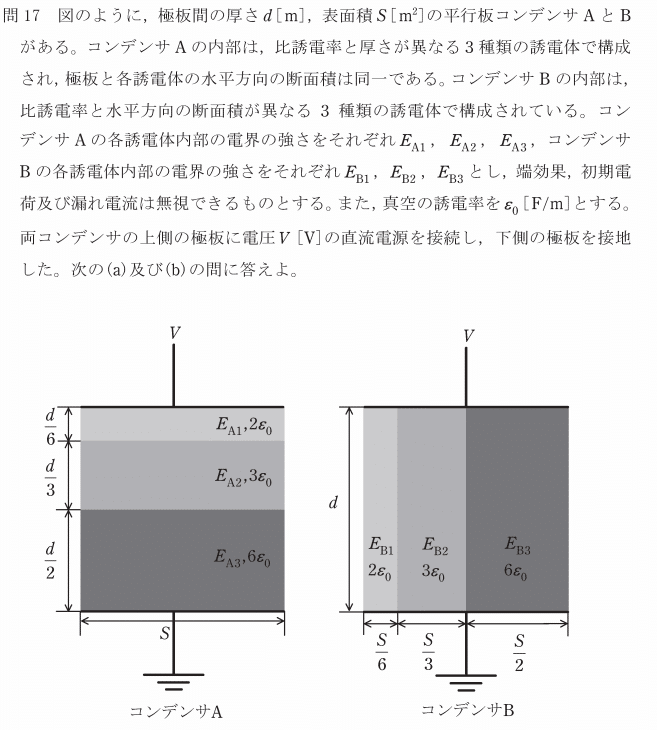

(a)

直列のコンデンサですね。
まずは電界の強度の大小関係
を求めていきます。
コンデンサの公式
\(\displaystyle Q=CV\) ①
Q:電荷 C:静電容量 V:電圧
\(\displaystyle V=Ed\) ②
E:電界 d:電極間距離
\(\displaystyle C=\frac{ε_0S}{d}\) ②
ε0:真空の誘電率 S:電極の面積(片側)
①式に②を入れると
\(\displaystyle Q=CEd\)
となります。
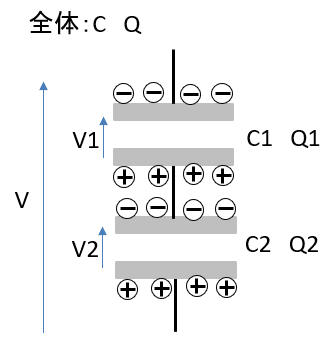
コンデンサ直列回路
電荷量Q=Q1=Q2
プラス+とマイナス-の電荷は一対一の関係になっています。
真ん中のプラスマイナスは足すと0なので全部の電荷量は等しいことがわかります。
わかりにくいかな?
電圧V=V1+V2
合成静電容量\(\displaystyle \frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}\)
※コンデンサが3つの直列でもやり方は一緒です
では解いていきます
\(\displaystyle Q_{A1}=C_{A1} V_{A1}=C_{A1} E_{A1} d_{A1}\)
どのコンデンサも電荷量は一緒なので
\(\displaystyle Q_{A1}=C_{A1} E_{A1} d_{A1}= C_{A2} E_{A2} d_{A2}= C_{A3} E_{A3} d_{A3} \)
計算ミスを減らすために。。。
\(\displaystyle C_{A1} E_{A1} d_{A1}= C_{A1}d_{A1}E_{A1}=\frac{ε_{A1} S}{d_{A1}} d_{A1}E_{A1} \)
\(\displaystyle =ε_{A1} S E_{A1}\)
整理すると
\(\displaystyle ε_{A1} S E_{A1}= ε_{A2} S E_{A2} = ε_A2 S E_{A2} \)
面積Sも消せますね!
\(\displaystyle ε_{A1} E_{A1}= ε_{A2} E_{A2} = ε_A2 E_{A2} \)
数値を代入していきます
\(\displaystyle 2ε_0 E_{A1}= 3ε_0 E_{A2} = 6ε_0 E_{A2} \)
整理します
\(\displaystyle E_{A1}= \frac{3}{2}E_{A2} = 3E_{A2} \)
Eの大きさランキングは。。。
\(\displaystyle E_{A1}>E_{A2} >E_{A2} \)
となります。
次が、最大値の大きさなので \(\displaystyle E_{A1}\)の大きさを求めていきます
まずは \(\displaystyle V_{A1}\)を求めていきます
\(\displaystyle Q_{A1}=C_{A1} V_{A1}=C_{A} V_{A}\)
\(\displaystyle V_{A1}=\frac{C_{A}}{C_{A1}} V_{A}\) ③
計算長くなりそうなので個別にCを出していきます
\(\displaystyle \frac{1}{C_A}=\frac{1}{C_{A1}}+ \frac{1}{C_{A1}}+ \frac{1}{C_{A3}} \)
\(\displaystyle \frac{1}{C_A}=\frac{ C_{A1}C_{A2}+ C_{A1}C_{A3} + C_{A2}C_{A3} }{ C_{A1}C_{A2}C_{A3} }\)
\(\displaystyle C_{A}=\frac{C_{A1}C_{A2}C_{A3} }{C_{A1}C_{A2}+ C_{A1}C_{A3} + C_{A2}C_{A3} }\)
それぞれのCも出しておきます
\(\displaystyle C_{A1}=12\frac{ε_0S}{d}\)
\(\displaystyle C_{A2}=9\frac{ε_0S}{d}\)
\(\displaystyle C_{A3}=12\frac{ε_0S}{d}\)
③に代入
\(\displaystyle V_{A1}= \frac{C_{A1}C_{A2}C_{A3} }{C_{A1}C_{A2}+ C_{A1}C_{A3} + C_{A2}C_{A3} } ×\frac{1}{C_{A1}} V_{A}\)
\(\displaystyle = \frac{ 9\frac{ε_0S}{d} 12\frac{ε_0S}{d} }{ 12\frac{ε_0S}{d}9\frac{ε_0S}{d}+12\frac{ε_0S}{d}12\frac{ε_0S}{d}+9\frac{ε_0S}{d}12\frac{ε_0S}{d}} V_{A}\)
整理すると
\(\displaystyle V_{A1}= \frac{ 9 × 12 }{ 12×9+12×12+9×12}V_{A}\)
\(\displaystyle = \frac{9}{9+12+9}V_{A}= \frac{3}{10}V_{A} \)
\(\displaystyle E_{A1}=\frac{V_{A1}}{d_{A1}}= \frac{3}{10}V_{A} \frac{1}{\frac{d}{6}} \)
\(\displaystyle = \frac{9}{5d}V_{A} \)
ってことで正解は(4)です
長かった。。。笑 もっとスマートな解き方ありそう
(b)
コンデンサのエネルギーですね!
コンデンサのエネルギー
\(\displaystyle コンデンサのエネルギー[J]=\frac{1}{2}CV^2\)
運動エネルギーと同じです。
コンデンサは電気を貯めるので電圧Vを使うって覚えてください
コイルのエネルギー
\(\displaystyle コイルのエネルギー[J]=\frac{1}{2}LI^2\)
コイルは電流が流れるのを遅らせるので電流Iを使う
コンデンサAのエネルギーは
\(\displaystyle J_A=\frac{1}{2}C_AV^2\)
\(\displaystyle J_A=\frac{1}{2} \frac{ 12\frac{ε_0S}{d} 9\frac{ε_0S}{d} 12\frac{ε_0S}{d} }{ 12\frac{ε_0S}{d}9\frac{ε_0S}{d}+12\frac{ε_0S}{d}12\frac{ε_0S}{d}+9\frac{ε_0S}{d}12\frac{ε_0S}{d}} V^2\)
\(\displaystyle J_A=\frac{1}{2} \frac{12×9}{9+12+9} \frac{ε_0S}{d} V^2= \frac{9}{5} \frac{ε_0S }{d}V^2\)
次はコンデンサBです
コンデンサ並列回路
電気を貯めるタンクが並列につながっているので足し算でOKです
合成静電容量C=C1+C2
\(\displaystyle C_B=C_{B1}+C_{B2}+C_{B3}\)
\(\displaystyle =\frac{ε_0 S}{3d}+ \frac{ε_0 S}{d} + \frac{3ε_0 S}{d} \)
\(\displaystyle =\frac{13ε_0 S}{3d}\)
\(\displaystyle J_B=\frac{1}{2}×\frac{13ε_0 S}{3d} V^2\)
\(\displaystyle = \frac{13}{6} \frac{ε_0 S}{d} V^2\)
エネルギーはコンデンサAはコンデンサBの何倍か?
\(\displaystyle \frac{J_A}{J_B} =\frac{ \frac{9}{5} \frac{ε_0S }{d}V^2 }{ \frac{13}{6} \frac{ε_0 S}{d} V^2 }= \frac{9×6}{5×13}=0.83 \)
正解は(2)です



コメント