令和3年理論 問7 第三種電気主任技術者試験 最小値の定理
簡単な問題かなーと思ったのですが癖がありますね。
可変抵抗がどうたらって問題と関係あるのかなーなんて思ってたら
がっつり問題の重要なポイントでした。さて解いていきましょう。
問題
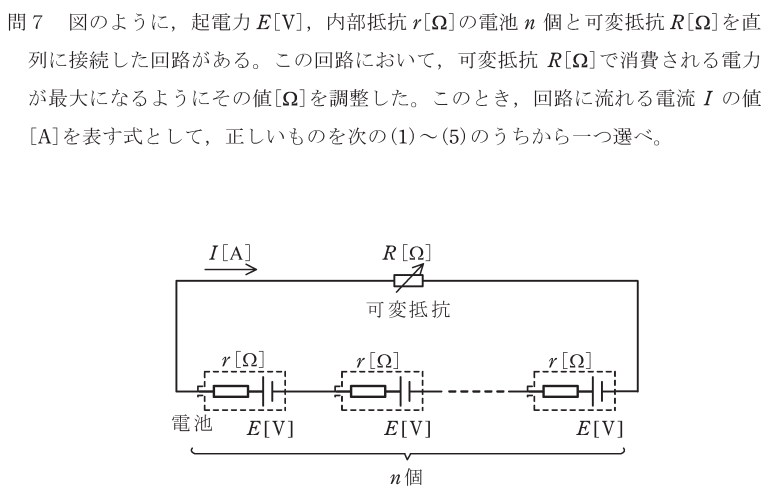
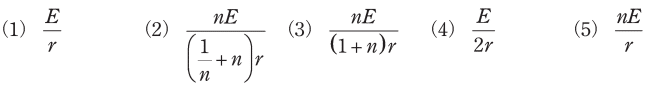
丁寧に解いていく
まずは、電池がn子直列につながってるのでまとめていきます。
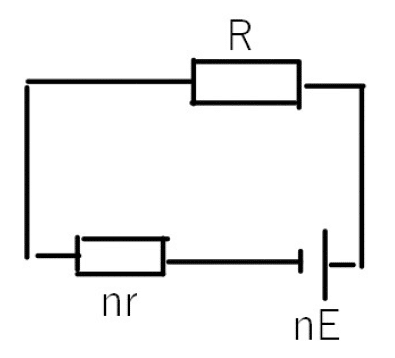
流れるIは
\(\displaystyle I=\frac{nE}{R+nr}\) ①
選択肢にRがないですね。
ここでポイントになるのが
可変抵抗Rで消費される電力が最大になるようにその値を調整した
です。
次にRに消費される電力を求めてみます
\(\displaystyle P=VI=I^2 R \)
さっきのI ① を代入して
\(\displaystyle P=(\frac{nE}{R+nr})^2 R\)
変数であるRについて整理していくと
\(\displaystyle =\frac{(nE)^2}{(R^2+2Rnr+{nr}^2)} R\)
\(\displaystyle =\frac{(nE)^2}{R+\frac{{nr}^2}{R}+2nr} \)
電力が最大値になるようにしたってことは、
分母にある\(\displaystyle R+\frac{{nr}^2}{R} \)が最小になるように決めればOKです
最小値だから\(\displaystyle R=\frac{{nr}^2}{R} \)
〇最小値の定理を使ってます
最後に説明しますね
\(\displaystyle R=nr \)が分母が最小になるRです
①式のRにnrを代入すると。。。
\(\displaystyle I=\frac{nE}{nr+nr}=\frac{E}{2r}\)
となります。
おまけ 最小値の定理
この公式は変圧器とかどの負荷率で最大効率になりますか?の問題とかで出てきます。
ながしーは
銅損=鉄損の時が効率最高!!と覚えていたので
今回の問題を解くとき少し驚きました。
さて、最小値の定理とは
〇最小値の定理
ab=一定 の時 x=y で
x+yは最小になる
最大値の定理っていうのもあるみたい
〇最大値の定理
a+b=一定 の時 a=b で
abは最大値をとる
最大値の定理は知りませんでした。
電験だとあまり使わない公式かもしれませんので覚えなくても良いかも。。。。



コメント