r3年電力 B問題 問17第三種電気主任技術者試験
単層2線式の電圧降下の問題です
ながしーはよく間違えるところ。。。
直流なのか交流なのか?
抵抗分だけでいいのか?リアクタンスを使うのか?
などなど悩んでしまいます。
皆様はきちんと押さえておいてください
問題
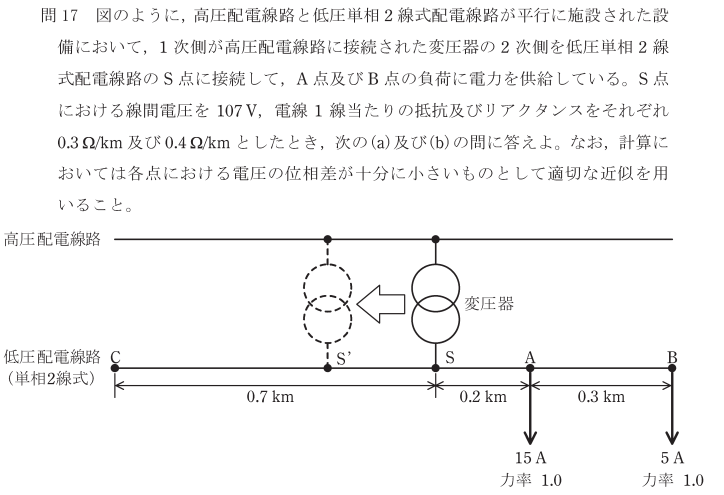

解答(1)
B点におけるS点に対する電圧降下率を求めていきます
まずはS-B間の電圧降下を求めます
単層2線式なので電圧降下の公式は
\(\rm \displaystyle ΔV=2I(RcosΘ+XsinΘ)\) ①
R:抵抗
X:リアクタンス
単層2線なので2倍しています
わからないのが、I、R、Xです。
力率1なのでcosΘ=1 sinΘ=0
S点からA点とA点からB点で数値が違うので
それぞれ計算していきます
まずRとXを計算します
S点からA点
\(\rm \displaystyle R_{SA}=0.2m×0.3Ω/m=0.06Ω\)
\(\rm \displaystyle X_{SA}=0.2m×0.4Ω/m=0.08Ω\)
A点からB点
\(\rm \displaystyle R_{AB}=0.3m×0.3Ω/m=0.09Ω\)
\(\rm \displaystyle X_{AB}=0.3m×0.4Ω/m=0.12Ω\)
Iを計算します。
負荷は
15A 力率1
5A 力率1
S点からA点の電流の大きさは
15A+5A=20A
A点からB点の電流の大きさは
5Aです。
図で書くと、このようなイメージです。
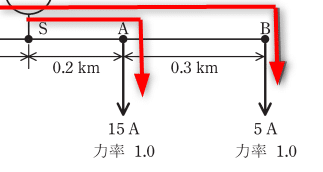
S点からA点の電圧降下
\(\rm \displaystyle ΔV_{SA}=2I_{SA}(R_{SA}cosΘ+X_{SA}sinΘ)\)
\(\rm \displaystyle =2×20A(0.06Ω×1+0.08Ω×0)\)
\(\rm \displaystyle =2.4V\)
A点からB点の電圧降下
\(\rm \displaystyle ΔV_{AB}=2I_{AB}(R_{AB}cosΘ+X_{AB}sinΘ)\)
\(\rm \displaystyle =2×5A(0.09Ω×1+0.12Ω×0)\)
\(\rm \displaystyle =0.9V\)
S点からB点の電圧降下は
2.4V*0.9V=3.3V
電圧降下率
\(\rm \displaystyle 電圧降下率=\frac{ΔV}{V_r}×100\)
\(\rm \displaystyle =\frac{V_s-V_r}{V_r}×100\)
ΔV:電圧降下 V
Vs:送電電圧 V
Vr:受電端電圧 V
Δ/Vsじゃないので注意!!
B点におけるS点に対する電圧降下率は
Vr=107V-3.3Vなので
\(\rm \displaystyle 電圧降下率_{SB}=\frac{3.3V}{107-3.3}×100=3.1822\)
正解は(2)です
解答(2)
\(\rm \displaystyle ΔV_{CS’}= ΔV_{S’B}\)
となる移動距離を求めます
\(\rm \displaystyle ΔV_{CS’}=2I _{CS’} (RcosΘ _{CS’}+XsinΘ _{CS’})\)
\(\rm \displaystyle ΔV_{S’B}= ΔV_{S’B} + ΔV_{AB} \)
\(\rm \displaystyle =2I _{S’A} (RcosΘ _{S’A}+XsinΘ _{S’A})+ ΔV_{AB} \)
ΔVABは(1)で求めているので省略します
移動距離をxと置いて、わかっている数値を代入します
cosΘ=0.8だったらsinΘ=0.6
cosΘ=0.6だったらsinΘ=0.8
よく出るので覚えておくと計算が早くなります
\(\rm \displaystyle ΔV_{CS’}= ΔV_{CS’}=2I _{CS’} (RcosΘ _{CS’}+XsinΘ _{CS’})\)
\(\rm \displaystyle =2×20(0.3Ω/km×(0.7km-x)0.8+0.4Ω/km×(0.7km-x)0.6)\)
\(\rm \displaystyle =13.44-19.2x\)
\(\rm \displaystyle ΔV_{S’B} =2I _{S’A} (RcosΘ _{S’A}+XsinΘ _{S’A})+ ΔV_{AB} \)
\(\rm \displaystyle =2×20( 0.3Ω/km×(x+0.2)×1+ 0.4Ω/km×(x+0.2)×0 )+ 0.9V \)
\(\rm \displaystyle =12x+3.3 \)
数値を代入する
\(\rm \displaystyle ΔV_{CS’}= ΔV_{S’B}\)
\(\rm \displaystyle 13.44-19.2x=12x+3.3 \)
\(\rm \displaystyle 31.2x = 10.14 \)
\(\rm \displaystyle x =0.325\)
正解は(3)です。



コメント