r3年理論 問15 第三種電気主任技術者試験
工夫された問題ですが、落ち着いて間違いないように正解したいですね。
Δ結合だったらちょっと無理だったかも。。。忘れている。
電流計を使用した問題です!
問題
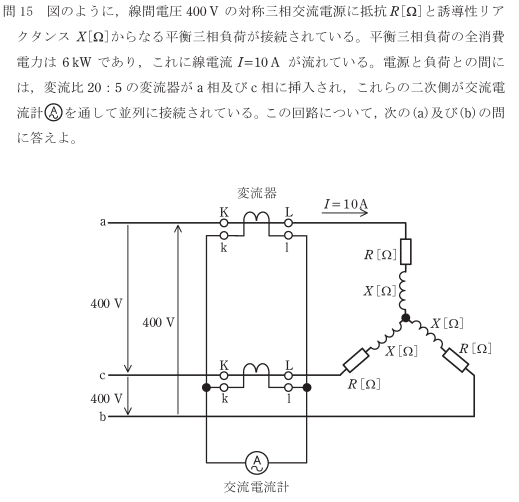

(a)

線電流が10A
変流比20:5 の先に電流計がついています。
なので線電流は変流比で小さくなってから電流計に送られます。
答え書いちゃってますが、下記の図のイメージです。
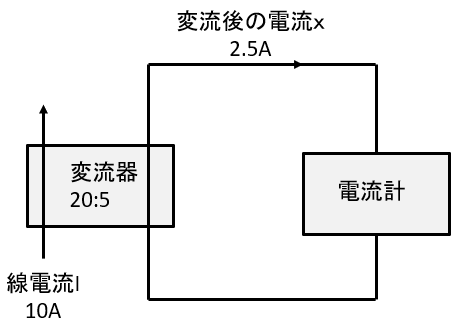
大電流だと扱いにくいし、電流計も大掛かりになるので変流器を使用して
小電流に変換してから測定するみたいです。
では解いていきます
\(\displaystyle 線電流10A:変流後の電流x=変流比20:5\)
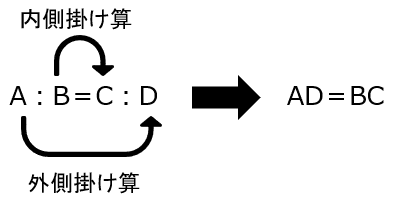
比の計算は下記のように行えばOK
図のようにやっていくと。。。
\(\displaystyle 線電流10A \times 5=変流後の電流x \times 10\)
\(\displaystyle 変流後の電流x= \frac{線電流10A \times 5}{20}=2.5A\)
正解は(2)
(b)
こちらは少し頭をひねります。
リアクタンスXを求めるから、、、リアクタンスを使う力率を使って考えます
\(\displaystyle 有効電力P=\sqrt{3} VI cosΘ\)
\(\displaystyle cosΘ=\frac{有効電力P}{\sqrt{3} VI} \)
\(\displaystyle cosΘ=\frac{6000W}{\sqrt{3} 400 \times 10} \)
=0.8661
となりました。
次、負荷のほうの力率を見てみますと
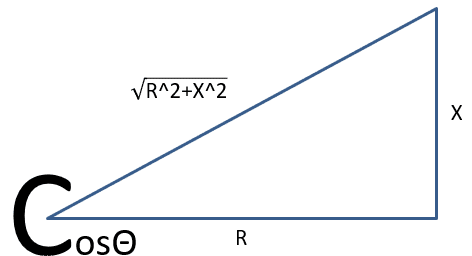
\(\displaystyle cosΘ=\frac{R}{ \sqrt{R^2+X^2} }\) ①
次。。。Rがわかりませんね
Rは線電流と抵抗と有効電力[kW]を使って求めていきます
有効電力は抵抗だけで消費されます
なのでRは
\(\displaystyle 有効電力=抵抗3つ \times I^2 R\)
\(\displaystyle R=\frac{有効電力}{抵抗3つ \times I^2}\)
\(\displaystyle R=\frac{6000W}{3 \times 10^2}=20Ω\)
となります。
①式にわかった項目を代入していくと
\(\displaystyle cosΘ=\frac{R}{\sqrt{R^2+X^2}}\)
\(\displaystyle 0.8661 =\frac{20}{\sqrt{20^2+X^2}}\)
\(\displaystyle (20^2+X^2) ={(\frac{0.8661}{20}})^2\)
\(\displaystyle X =11.54\)
正解は(1)



コメント