直流の合成抵抗について書いていきます。

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋
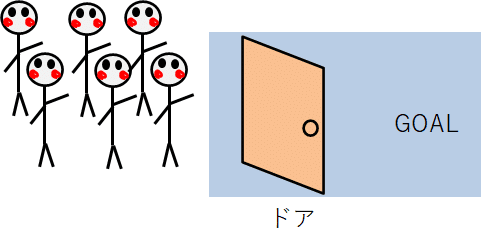
水車の絵が描けないのでドアで表現してみます。
・ながしー達はゴールに行きたい
・ドアがあるので、ドアを開けないとGOALに行けない
・ドアは一人づつしか通れない
・GOALに行くまでのドアは1個ある
・ドアを1人通るのに1秒かかる
ながしーが10人いるとすると全員がGOALに行くまでに
10人×1秒/人=10秒かかります。
1秒/人が抵抗のイメージです。
抵抗もRが1つなら
抵抗Rになります。

直列の場合
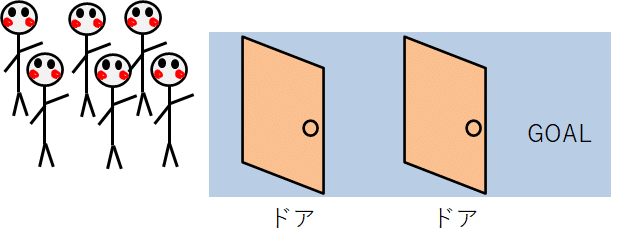
今度は
・ながしー達はゴールに行きたい
・ドアがあるので、ドアを開けないとGOALに行けない
・ドアは一人づつしか通れない
・GOALに行くまでのドアは2個ある
・ドアを1人通るのに1秒かかる
ながしーが10人いるとすると全員がGOALに行くまでに
10人×2秒/人=20秒かかります。
1秒/人+1秒/人=2秒/人です。
抵抗が直列に接続されていると
\(R+R=2R\)となります
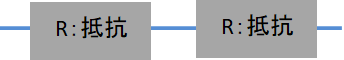
上の2つの直列の抵抗は下図の2Rに変換されます。

3つ以上でも同様です

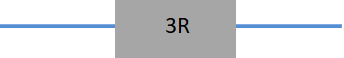
合成抵抗は3Rです
直列の抵抗は足し算でOK
\(合成抵抗R_0=R_1+R_2+R_3+・・・・・R_n\)
並列の場合(2つの抵抗の場合)
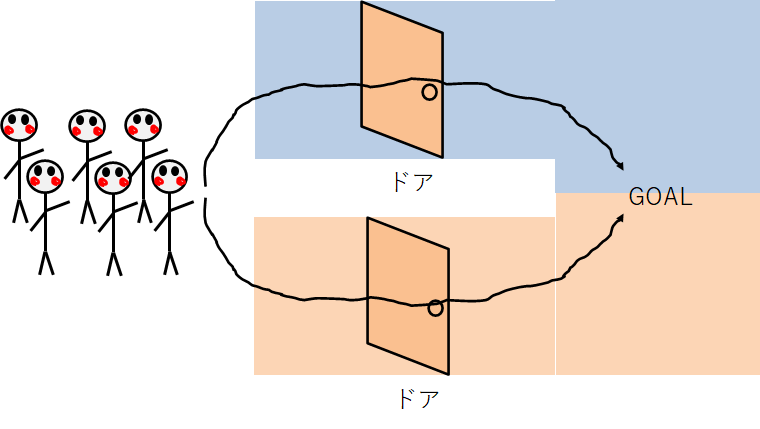
今度は並列バージョンです。
・GOALに行くまでのドアは2個ある
・ドアを1人通るのに1秒かかる
・ゴールに行くルートは2つ
・ながしーが10人いる
今回は並列にドアがあるので2人づつ行くことができます!
・1秒あたり2人いけるので 0.5秒/人
全員がGOALするまでに
10人×0.5秒/人=5秒かかります。
ドアが多いのにたくさん通過できましたね。
何故でしょうか?
経路が2つあるので通りやすいんですね!
次に抵抗で見てみます。
並列の抵抗は。。。

このように変換されます。
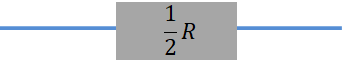
1/2Rです。
初めのRより小さくなっています。
先ほど話したように経路が2つあるので通りやすくなっているんですね。
公式は
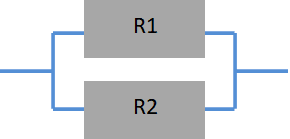
抵抗が2個並列になっている場合の公式
和分の積
\(\displaystyle 合成抵抗R_0=\frac{R_1 \times R_2}{R_1+R_2}\)
どっちが足し算でどっちが掛け算か忘れたとき
\(R_1=1 、R_2=1\)と考えて、小さくなったほうが正解です。
実際に計算してみると。。。
\(\displaystyle R_0=\frac{R \times R}{R+R}=\frac{R^2}{2R}=\frac{R}{2}\)
並列(2つ以上場合)の計算
今回は4つの並列抵抗で考えていきます。
〇まずドアで考えてみます。
・GOALに行くまでのドアは5個ある
・ドアを1人通るのに1秒かかる
・ゴールに行くルートは2つ
・ながしーが10人いる
並列にドアがあるので5人づつ行くことができます!
・1秒あたり2人いけるので 0.2秒/人
全員がGOALするまでに
10人×0.2秒/人=2秒かかります。
並列は数が多ければ多いほど通りやすくなるんですね。
並列の合成抵抗の公式
\(\displaystyle \frac{1}{R_0}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+・・・・+\frac{1}{R_n}\)
合成抵抗の逆数になっているので最後にひっくり返してね!
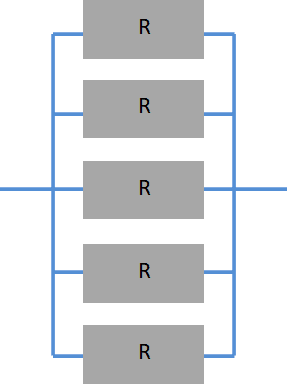
計算してみましょう
\(\displaystyle \frac{1}{R_0}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R}
=\frac{5}{R}\)
最後にひっくり返しておしまいです
\(\displaystyle R_0=\frac{R}{5}\)
和分の積をひたすら繰り返してもOKです。
ながしーはよくやります。。。
まとめ
直列の合成抵抗
直列の抵抗は足し算でOK
\(合成抵抗R_0=R_1+R_2+R_3+・・・・・R_n\)
並列の合成抵抗(2つの場合)
和分の積
\(\displaystyle 合成抵抗R_0=\frac{R_1 \times R_2}{R_1+R_2}\)
どっちが足し算でどっちが掛け算か忘れたとき
\(R_1=1 、R_2=1\)と考えて、小さくなったほうが正解です。
並列の合成抵抗
並列の合成抵抗の公式
\(\displaystyle \frac{1}{R_0}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+・・・・+\frac{1}{R_n}\)

他にも過去問解いていますよ
国家資格・電気・エネ管・電験のお部屋



コメント